The General Equilibrium Model of International-National Interactions between Economy, Energy and the Environment (GEMINI-E3)

Short overview

GEMINI-E3 is a multi-country, multi-sector, recursive computable general equilibrium (CGE) model. It simulates all relevant markets, domestic and international, considered as perfectly competitive, which implies that the corresponding prices are flexible in markets for commodities (through relative prices), for labour (through wages), and for domestic and international savings (through rates of interest and exchange rates). Time periods are linked in the model through endogenous real rates of interest determined through the balancing of savings and investment. National and regional models are linked by endogenous real exchange rates resulting from constraints on foreign trade deficits or surpluses. There is one notable—and usual—exception to this general assumption of perfect competition, which concerns foreign trade. Goods of the same sector produced by the different countries are not supposed to be perfectly competitive; they are considered as economically different goods, more or less substitute according to an elasticity of substitution known as the Armington assumption. The main outputs of the GEMINI-E3 model are on a country and annual basis: carbon taxes, marginal abatement costs and prices of tradable permits (when relevant), effective abatement of CO₂ emissions, net sales of tradable permits (when relevant), total net welfare loss and components (net loss from terms of trade, pure deadweight loss of taxation, and net purchases of tradable permits when relevant), macro-economic aggregates (e.g. production, imports and final demand), real exchange rates and real interest rates, and data at the industrial level (e.g. change in production and in factors of production, and prices of goods).

Key features of the GEMINI-E3 model

Geographic coverage

In the version of GEMINI-E3 to be used in the PARIS REINFORCE project, the model divides the world into five countries (USA, China, India, Brazil and Russia) and six aggregated regions, with EU-28 being one. The following table gives the regional coverage of the model.

Regional representation and countries included in each region in GEMINI-E3
Region ID	Geographic region	Countries
USA	United States of America	United States of America
EUR	European Union (28)	Austria, Belgium, Bulgaria, Croatia, Cyprus, Czech Republic, Denmark, Estonia, Finland, France, Germany, Greece, Hungary, Ireland, Italy, Latvia, Lithuania, Luxembourg, Malta, Netherlands, Poland, Portugal, Romania, Slovakia, Slovenia, Spain, Sweden, United Kingdom
CHI	China	China, Hong Kong
IND	India	India
BRA	Brazil	Brazil
RUS	Russia	Russia
CSA	Central and South America countries	Mexico, Argentina, Bolivia, Chile, Colombia, Ecuador, Paraguay, Peru, Uruguay, Venezuela, Costa Rica, Guatemala, Honduras, Nicaragua, Panama, El Salvador, Dominican Republic, Jamaica, Puerto Rico, Trinidad and Tobago, Caribbean, Rest of North America, Rest of South America, Rest of Central America
ASI	Other Asian countries	Japan, South Korea, Mongolia, Taiwan, Brunei Darussalam, Cambodia, Indonesia, Laos, Malaysia, Philippines, Singapore, Thailand, Viet Nam, Bangladesh, Nepal, Pakistan, Sri Lanka, Rest of East Asia, Rest of South Asia
MID	Middle East	Bahrain, Iran, Jordan, Kuwait, Oman, Qatar, Saudi Arabia, Turkey, United Arab Emirates, Rest of Western Asia
AFR	Africa	Egypt, Morocco, Tunisia, Benin, Burkina Faso, Cameroon, Cote d’Ivoire, Central Africa, South Central Africa, Ghana, Guinea, Nigeria, Senegal, Togo, Central Africa, South Central Africa, Ethiopia, Kenya, Madagascar, Malawi, Mauritius, Mozambique, Rwanda, Tanzania, Uganda, Zambia, Zimbabwe, Botswana, Namibia, South Africa, Rest of Western Africa, Rest of South African Customs
ROW	Rest of the World	Australia, New Zealand, Canada, Switzerland, Norway, Albania, Belarus, Ukraine, Kazakhstan, Kyrgyzstan, Tajikistan, Armenia, Azerbaijan, Georgia, Israel, Rest of Oceania, Rest of Former Soviet Union, Rest of the World

Economic activities coverage

Like other CGE models, GEMINI-E3 covers all economic activities. In this version, the model divides the economy into eleven sectors, each one of which produces a good. Five of the sectors are related to the energy sector, three represent the transport sector, one covers the energy-intensive industries, and the remaining two sectors are agriculture and other goods and services. The following table provides the detailed industrial classification of GEMINI-E3.

List of economic activities covered by GEMINI-E3
Sector ID	Sector
01	Coal
02	Crude oil
03	Natural Gas
04	Refined petroleum products
05	Electricity
06	Agriculture
07	Energy intensive industries
08	Other goods and services
09	Land sector
10	Sea transport
11	Air transport

Energy system coverage

The energy sectors are represented similarly to other economic sectors by using nested CES functions.

For electricity production, GEMINI-E3 distinguishes fossil fuel (i.e. coal, natural gas and oil power plants), nuclear, hydro, solar and wind power plants. Power generation is separated from the other activities (transmission and distribution) that appear through their factors of production at the top of the nesting structure. Power generation involves only two factors of production: capital and fuel for fossil fuel power plants and capital and a resource for renewables. With this nesting structure it is possible to better take into account the power generation portfolio and to represent inter-fuel substitutability as well as substitutability between fossil and renewable power generation. The model allows the use of carbon capture and storage (CCS) technology for coal and gas power plants when the carbon price is above the full cost of CCS.

Coal, crude oil and natural gas sectors include a fixed factor that represents the non-renewable resource associated with each fossil fuel energy. For these sectors we suppose that the domestic production is realised with this fixed factor and the other standard inputs (i.e. capital, labour, material and energy) through, again, a nested CES function.

Finally, refined petroleum products are produced from the basic input, i.e. crude oil. The model considers this specificity with a CES function between crude oil and other standards inputs at the top level of the nested CES structure.

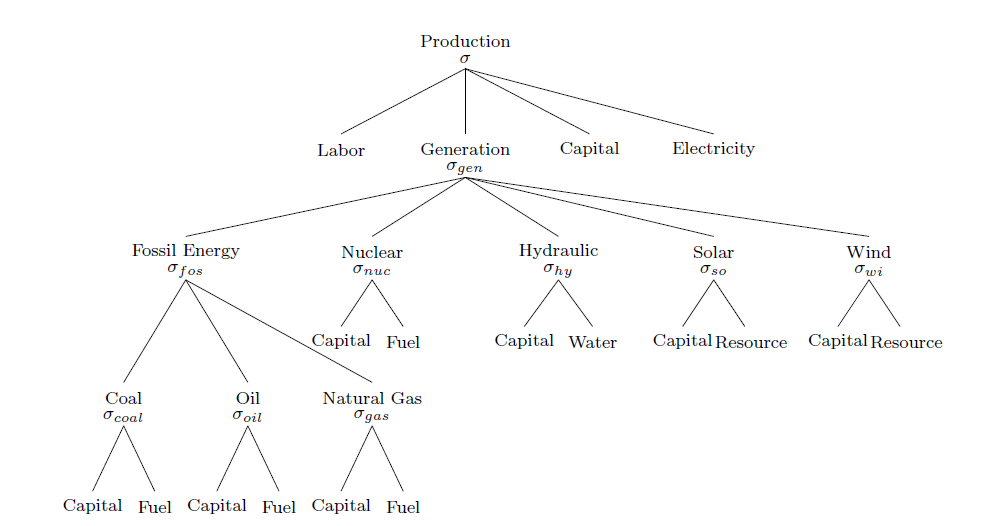
Nested CES production structure – Electricity in GEMINI-E3

Time periods

GEMINI-E3 is a recursive-dynamic, yearly model, with backward-looking (adaptive) expectations. The model simulates the global economy up to 2050. The base year of the model is 2014.

Database

The building and calibration of the CGE model rest on economic and energy data that are usually contained in comprehensive databases, specially established for this purpose. In particular, this version of GEMINI-E3 is built on GTAP-10 (Aguiar et al. 2019), a database that accommodates a consistent representation of energy markets in physical units (tons of oil equivalent) as well as detailed socio-accounting matrices in USD for a large set of countries or regions and bilateral trade flows. The GTAP database is completed by other information especially on indirect taxation and government expenditures, mainly coming from the International Energy Agency (IEA), OECD and the International Monetary Fund. Important efforts have been put into harmonising all these sources of information. The result is a consistent social accounting matrix for each country/region.

Emissions granularity

Carbon emissions are directly computed from fossil energy consumption in physical quantities using coefficient factors that differ among firms (i.e. sectors), households and regions.

The representation of non-CO₂ emissions is based on the GTAP Non-CO₂ GHG emissions (NCGG) dataset (Rose and Lee, 2008). The database distinguishes several emissions of methane (CH₄), nitrous oxide (N₂O) and fluorinated gases. The emissions of each source are linked to an activity level (or an economic driver). Abatements by gases are computed from the EPA abatement curves (EPA 2013).

Forests can mitigate GHGs by storing carbon, therefore GEMINI-E3 computes carbon sequestered by forest. We use forest mitigation supply functions computed by Favero et al. (2018), which use the Global Timber Model (GTM) to simulate the optimal management of forest land for climate change mitigation under several carbon price paths. These supply curves allow to compute the carbon sequestered by forest in each region.

Socioeconomic dimensions

As other global macroeconomic models, GEMINI-E3 determines endogenously all economic variables by sectors, regions and years. The model computes the level of production (and the inputs associated: labour, capital, energy, and materials) but also demand (household demand, investment and export) by sectors/goods and regions. The prices associated to each good are determined endogenously. However, the dynamic of the model in the baseline scenario is mainly driven by exogenous variables that are listed hereafter.

Demographic assumptions

Population growth is exogenous and based on a forecast by the United Nations (United Nations 2019). The medium variant projection is usually retained. These projections allow to determine the growth of the labour supply using assumptions on participation rates by sex and age.

Technical progress and energy resources

Economic growth (i.e. GDP growth) and international energy prices (i.e. crude oil price, natural gas and coal prices) are usually based on IEA’s forecasts in its World Energy Outlook (IEA, 2018). Technical progresses on labour as well as the dynamic of the energy resources are calibrated in order to reproduces the figures given by the World Energy Outlook.

Autonomous energy efficiency improvement

Finally, assumptions on technical progresses associated with energy consumption (i.e. autonomous energy improvement) are determined exogenously and usually calibrated on past data.

Economic indicators

GDP
Households and government consumptions
Investment
Exports and imports
Government saving

These variables are expressed in volume (i.e. at the base year prices), but the prices associated to each of these macroeconomic aggregates are also computed (prices of GDP, of household consumption, etc.).

Production by sector
Demand by sector and by usage (final demand, intermediate use)
Production factors by sector (labour demand, energy consumption, capital, etc.

Again, for these sectoral data, changes in price and in volume are computed.

Finally, the model gives the international flows of goods and services (i.e. imports and exports) between the regions/countries described by the model.

Calibration of the model

The elasticities of substitution used in the supply and demand functions (i.e. in the nested CES functions) are based on a literature review. The other coefficients of the model are calibrated in order to reproduce exactly the reference year, i.e. 2014.

Economic rationale and model solution

For each sector and region, the model computes total demand as the sum of final demand (investment, consumption and exports) and intermediate consumptions by all sectors. Then, demand is split between imports and domestic production according to the Armington assumption. Domestic production technologies are described through nested CES functions, which differ according to the sector. For example, the following figure shows the nested CES production structure of the sector producing “other goods and services”. Production is done with four aggregates: capital, labour, material and energy. In a second step (nest), material and energy are decomposed in individual goods using again CES functions.

Nested CES production structure - Other goods and services in GEMINI-E3

Household behaviour consists of three interdependent decisions: 1) labour supply; 2) savings; and 3) consumption of the various goods and services. In GEMINI-E3, both labour supply and the rate of savings are assumed to be exogenous. Demand in the different commodities has prices of consumption and income (more precisely "spent" income, i.e. income after savings) as arguments and is derived from nested CES utility functions. At the first level of the consumption function, households choose between three aggregates: housing, transport and other consumptions. Energy consumption is split into two parts: for transportation and housing purposes. Transport demand is split into purchased and own transports. The model distinguishes three types of personal vehicles depending on the fuel used. Electric vehicles (EV), which are mainly dedicated to short or medium distance, and two other types using the same motorisation (i.e. internal combustion, or IC), one using petroleum products and the other biofuels. Each vehicle is characterised by a vehicle capital (called powertrain in the following figure) and a type of fuel used (refined oil, biofuel or electricity).

Total government consumption is exogenous and its evolution over time, determined in the calibration of the model, is driven by the growth rates of the main aggregates of the economy. The model splits total consumption between goods based on fixed budget shares.

The exports are the sum of imports by all other countries/regions that are endogenously determined in the model.

Investment by products is derived from investment by sectors through a transfer matrix. Investment by sector is determined from an "anticipated" capital demand using the CES function of each sector. Anticipated production prices and demands are based on adaptive expectations.

The government surplus or deficit is the difference between revenues accruing from taxation (direct and indirect, including social security contributions) and expenditures that are of two types: public consumption and transfers to households (mainly social benefits).

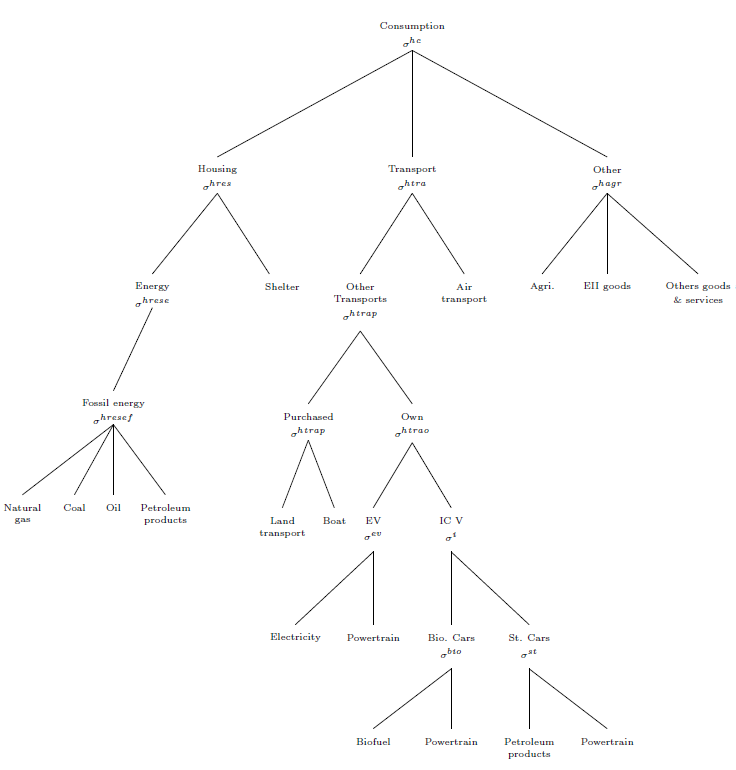
Nested CES Household consumption in GEMINI-E3

Policy questions and SDGs

Key policies that can be addressed

First, based on climate targets (or pathways) as the ones defined by COP21 (see Babonneau et al., 2018a), the model can evaluate the carbon prices that will be needed to reach these goals.
However, the model can also evaluate the impact on GHG emissions associated to a carbon tax defined by government (see Babonneau et al., 2018c).

Climate change policies can be evaluated through the implementation of a carbon tax or an emissions trading system. The carbon tax can be uniform among countries/regions and sectors or be differentiated. The model can simulate a carbon tax framework coupled with an emissions trading system (see Babonneau et al., 2018b). Within these climate policies, other constraints such as nuclear moratorium or non-price policies (such as emission standards) can also be analysed (see Babonneau et al., 2018c).

Usually the carbon tax revenue is recycled by the government to households through a lump sum transfer in order to keep constant the surplus or deficit of the government. But other recycling rules can be implemented in the model.

GEMINI-E3 computes not only the carbon prices associated to climate change policies but also welfare changes. A consistent measure of welfare cost is the household’s surplus. Deriving demand by households from a utility function then allows one to have a direct economic measure of the welfare cost of abatement policies. Households surplus may be directly reckoned from the numerical results of scenarios, for every year and every country/region, and they can be aggregated in various ways: either weighted by exchange rates and summed for a given year or period, or discounted through interest rates for a given country and then measuring the total discounted cost of the abatement policy. To eliminate the effects of changes in the relative prices of foreign trade, one must subtract the marginal gain (or loss) from changes in the terms of trade (GTT) to marginal welfare loss. This yields the so-called deadweight loss (DWL) of taxation. The GTTs represent spill-over effects due to changes in international prices. In a climate change policy, these GTTs come mainly from the drop in fossil energy prices that result from the decrease of world energy demand.

Implications for other SDGs

GEMINI-E3 was not originally designed to assess the sustainable development goals (SDGs). However, some indicators related to economic growth (SDG8), energy (SDG7) and climate (SDG13) can be evaluated directly from outputs of the model. Some other indicators may be analysed by performing some computations outside the model or by coupling GEMINI-E3 with other models.

Recent use cases

List of recent publications using the GEMINI-E3 model
Paper	Topic	Key findings
Vöhringer et al. (2019)	Analysis of economic consequences of climates in Switzerland, by covering health, buildings/infrastructure, energy, water, agriculture, and tourism, as well as the spill-overs to other sectors, and international effects	For the considered impacts, welfare decreases by 0.37% to 1.37% in 2060 relative to a reference without climate change. Higher summer temperatures increase mortality and decrease productivity. Contrariwise, tourism benefits from extended summer seasons. Regarding energy, increased demand for cooling is overcompensated by savings in heating.
Babonneau et al. (2018a)	Evaluation of the Paris Intended Nationally Determined Contributions (INDCs) and the design of fair agreements concerning additional abatements up to 2050	The analysis confirms the weakness of INDC pledges Nevertheless, we show that, with political determination, an equitable burden-sharing agreement can be achieved with very reasonable costs for all nations of approximately 0.8% of total discounted household consumption. With a more ambitious 1.5°C target, global cost is multiplied by a factor of four revealing the stringency of such an objective.
Babonneau et al. (2018b)	Evaluation of the recent developments of European climate policy from the perspective of the 2030 and 2050 European commitments; analysis of the European Effort Sharing Decision (ESD) proposed in July 2016 and of its cost per member state by 2030; considering the Brexit referendum that took place in June 23, 2016 in the United Kingdom	Results show that the EU burden-sharing based on GDP per capita implies very large discrepancies between Member States. If United Kingdom (UK) implements a Brexit, the 27 European countries could experience some welfare costs as additional abatements are required by the non-participation of UK to the ESD rules. In 2030, this additional cost is estimated at 8 billion € within a full Brexit. However, this cost is less significant than the one supported by UK which is approximately equal to 15 billion € in 2030.
Labriet et al. (2015)	Analysis of the impacts of changes in future temperatures on the heating and cooling services of buildings and the resulting energy and macro-economic effects at global and regional levels	At the global level, the climate feedback induced by adaptation of the energy system to heating and cooling is found to be insignificant, partly because heating and cooling-induced changes compensate and partly because they represent a limited share of total final energy consumption. However, significant changes are observed at regional levels, more particularly in terms of additional power capacity required to satisfy additional cooling services, resulting in increases in electricity prices.
Babonneau et al. (2018c)	Analysis of deep decarbonisation pathways for a small open economy (Switzerland) that lacks the usual avenues for large CO2 reductions—heavy industry and power generation	Results show that the ambitious target is attainable at moderate welfare costs, even if it needs very high carbon prices, and that these costs are lower when either CO2 can be captured and sequestered, or electricity consumption can be taxed sufficiently to stabilise it.
Joshi et al., (2016)	Assessment of the physical and economic consequences of sea-level rise (SLR) in the twenty first century	The simulation results suggest that the potential development of future coastal areas is a greater source of uncertainty than the parameters of SLR itself in terms of the economic consequences of SLR. At global level, the economic impact of SLR could be significant when loss of productive land along with loss of capital and forced displacement of populations are considered. Furthermore, highly urbanised and densely populated coastal areas of South East Asia, Australia and New Zealand are likely to suffer significantly if no protective measures are taken.

References

Aguiar, A., Chepeliev, M., Corong, E. L., McDougall, R., & van der Mensbrugghe, D. (2019). The GTAP data base: version 10. Journal of Global Economic Analysis, 4(1), 1-27.

Favero, A., Sohngen, B., Huang, Y., & Jin, Y. (2018). Global cost estimates of forest climate mitigation with albedo: a new integrative policy approach. Environmental Research Letters, 13(12), 125002.

Babonneau, F., Haurie, A., & Vielle, M. (2018). From COP21 pledges to a fair 2 C pathway. Economics of Energy & Environmental Policy, 7(2).

Babonneau, F., Thalmann, P., & Vielle, M. (2018). Defining deep decarbonization pathways for Switzerland: an economic evaluation. Climate Policy, 18(1), 1-13.

Babonneau, F., Haurie, A., & Vielle, M. (2018). Welfare implications of EU effort sharing decision and possible impact of a hard Brexit. Energy Economics, 74, 470-489.

Vöhringer, F., Vielle, M., Thalmann, P., Frehner, A., Knoke, W., Stocker, D., & Thurm, B. (2019). Costs And Benefits Of Climate Change In Switzerland. Climate Change Economics, 10(02), 1950005.

Labriet, M., Joshi, S. R., Vielle, M., Holden, P. B., Edwards, N. R., Kanudia, A., ... & Babonneau, F. (2015). Worldwide impacts of climate change on energy for heating and cooling. Mitigation and Adaptation Strategies for Global Change, 20(7), 1111-1136.

Joshi, S. R., Vielle, M., Babonneau, F., Edwards, N. R., & Holden, P. B. (2016). Physical and economic consequences of sea-level rise: A coupled GIS and CGE analysis under uncertainties. Environmental and Resource Economics, 65(4), 813-839.